Longest Increasing Subsequence

300. Longest Increasing Subsequence

Solution: nlog(n) solution requires first understanding the O(n^2) solution.

We obviously need to go through every element in nums to get the answer, which requires O(n) time. To achieve O(nlogn), we need to think about how to avoid traverse the entire dp array (which stores answers to smaller subproblems). We can build another array d to store the best values (i.e., the minimum values for LIS of lengths 1, 2, 3, etc.) we’ve seen so far, using patience sort. Below is one example:

Input: [10,9,2,5,3,7,101,18]

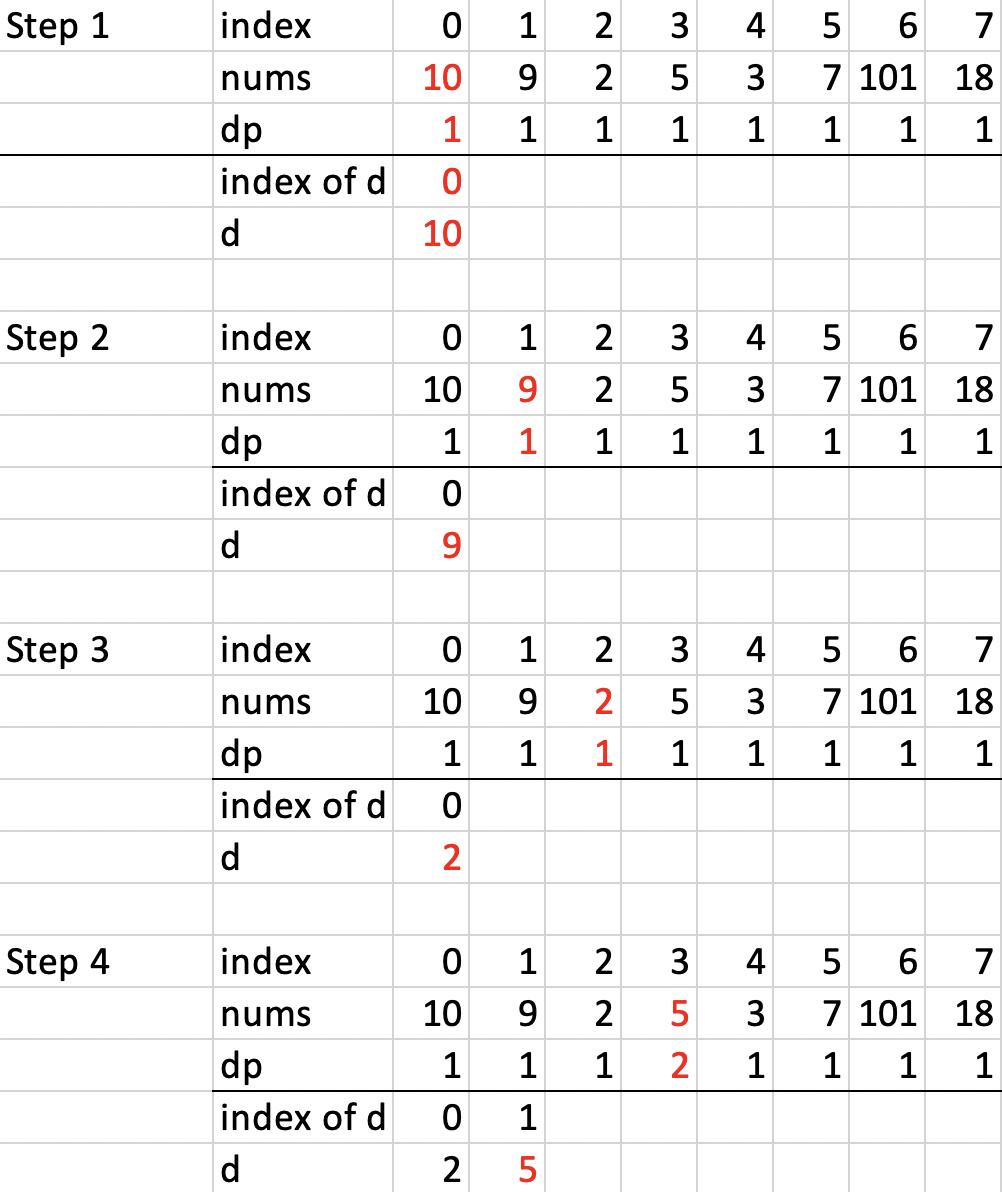
Step 1: Just by looking at the first element, we can tell that—for the smallest subproblem (where there’s only 1 number in nums)—the LIS so far is just 1.

Step 2: 9 is smaller than 10, so LIS still has the same length 1 but we can keep 9 in d as this gives us a better chance to find a longer sequence.

Step 3: 2 is smaller than 9, so LIS still has the same length 1 we we can keep 2 in d as this gives us a better chance to find a longer sequence.

Step 4: 5 is greater than 2, so the current length of LIS increases by 1.

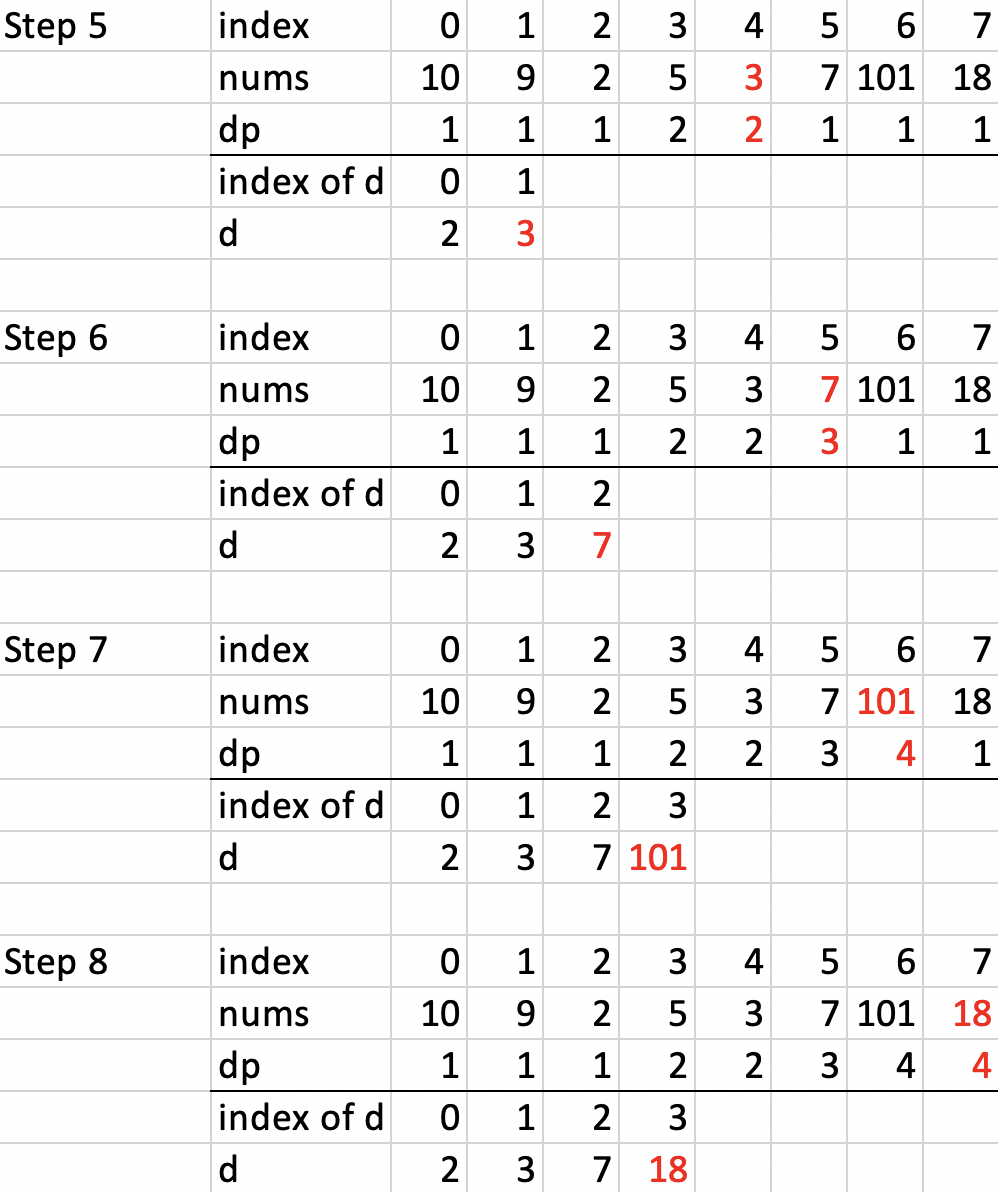
Step 5: 3 is greater than 2 (though it’s not greater than 5), so the current length of LIS keeps the same but we keep 3 in d as this gives us a better chance to find a longer sequence.

Step 6: 7 is greater than 5, so the current length of LIS increases by 1 and we also want to store this 7 in the d.

Step 7: 101 is greater than 7 (and also greater than other elements previous to 101), so the current length of LIS increases by 1. We also want to store this in d.

Step 8: 18 is great than 7. (Well, it’s greater than everything else except for 101), so the current length of LIS is 3 (counting from 7 in num) + 1.

We’re done. The last element in dp (which equals the length of d) is the answer!

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        L = len(nums)
        if L == 0: return 0
        
        d = [nums[0]]
        dp = [1] * L
        
        for i in range(1, L):
            if nums[i] > d[-1]:
                d.append(nums[i])
                
            elif nums[i] < d[-1]:
                pos = bisect.bisect_left(d, nums[i])
                if d[pos] != nums[i]:
                    d[pos] = nums[i]
            dp[i] = len(d)

        return(dp[-1])